
the ac voltage across the capacitor is readily computed. We know that the Fourier transform of a Gaus- sian: f(t) e t. # \\ # And additional item: If you are familiar with ac circuit analysis, try comparing the result that you get from the linear response theory with that from computing the ac impedances of the two components and considering it as a voltage divider problem-i.e. Translated to our notation, this would give: Starting with the claim and applying the FT inversion formula on both sides we obtain: Now with the definition of the convolution we get: multiplying the RHS with we have: Because we can use Fubini on the integrals above, which gives us: from which. This property states that the convolution of signals in the time domain will be transformed into the multiplication of their Fourier transforms in the. Conv Function 1/3 for xi-1 1/3 for xi 1/3 for xi+1 Here, we slide our convolution function along 3-points along the original function.


Looking back at your original question, it's not clear what you're trying to do. Found the solution on: Fourier Transform Proof. Convolve: apply a convolution function along some window/subset of the original function This convolution function specifies the weights that you use to compute your average Ex.
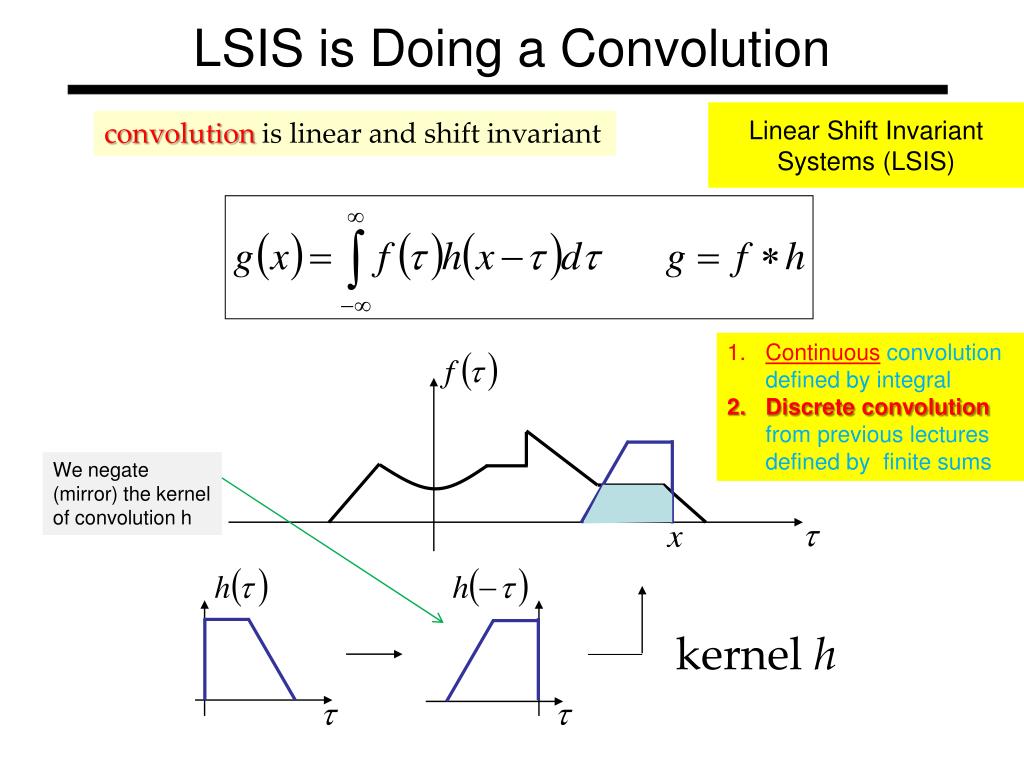
Incidentally, if # H(t) # is the response to a unit step function, # h(t)=\frac # for # t>0 #. Then ZJW is coded as some scaled value of the convolution of x(t) and y(t), which doesn't really follow assuming that ZJW is supposed to be the Fourier transform of z(t).


 0 kommentar(er)
0 kommentar(er)
